ChatGPT, et après ? Bilan et perspectives de l'intelligence artificielle

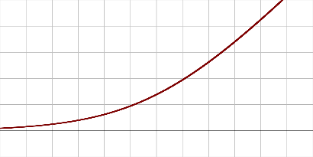
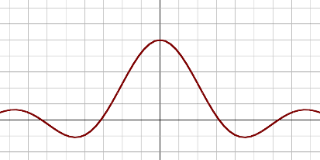
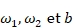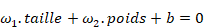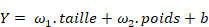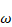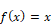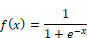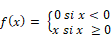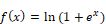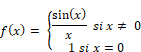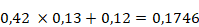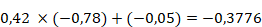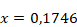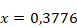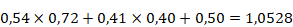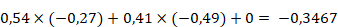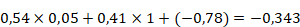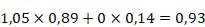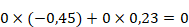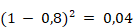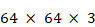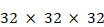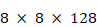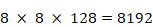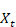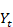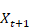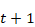C. LA SUMMA DIVISIO DE L'IA : INTELLIGENCE ARTIFICIELLE SYMBOLIQUE ET INTELLIGENCE ARTIFICIELLE CONNEXIONNISTE

1. L'intelligence artificielle symbolique

a) Principes généraux des IA symboliques

L'intelligence artificielle symbolique constitue, d'un point de vue historique, la première grande famille de technologies d'intelligence artificielle, caractérisée par l'utilisation de symboles et de règles logiques pour résoudre des problèmes au terme de déductions. Elle s'est surtout développée au cours des années 1960, 1970 et 1980.

Si elle existe toujours aujourd'hui, elle est largement éclipsée par les résultats spectaculaires de l'intelligence artificielle connexionniste. L'un des outils les plus importants de l'IA symbolique sont les « systèmes experts », appelés aussi systèmes à base de connaissances. Un système expert est un logiciel qui va extraire des connaissances à partir du savoir des experts humains d'un domaine et vise à reproduire les raisonnements pertinents de ces experts face à des cas particuliers.

Ces systèmes sont composés de trois parties : une base de faits, une base de règles et un moteur d'inférence (si tels faits, alors effectuer telles actions) : grâce aux faits et aux règles fournis en entrées, le modèle va utiliser le moteur d'inférence pour déduire de nouveaux faits et ainsi répondre à une problématique posée. Il s'agit d'un modèle déductif. La connaissance est donc décrite sous la forme générale de règles :

« SI Condition (s) » « ALORS Action (s) »

Ces systèmes analysent une représentation de la situation pour voir quelles règles sont pertinentes, résolvent les éventuels conflits si plusieurs règles s'appliquent et exécutent les actions indiquées en modifiant la situation en conséquence. Ces systèmes sont efficaces dans des domaines restreints mais deviennent difficiles à gérer quand ils doivent manipuler de nombreuses règles ou intervenir dans des domaines complexes, instables ou ouverts.

b) Quelques illustrations de ces technologies

Un exemple d'intelligence artificielle symbolique appliqué à la médecine est une IA destinée au diagnostic des maladies infectieuses du sang, le système expert MYCIN développé dans les années 1970 par l'université de Stanford^39(*). Cette IA spécialisée dans l'analyse de sang aide à identifier des infections bactériennes et propose des traitements.

Il avait pour objectif d'assister les médecins dans leur travail et de connaître des usages concrets. Son corpus de connaissances était constitué d'un ensemble de données médicales tandis que sa base de règles était composée de règles de type « si... et... alors... » ; par exemple de façon simplifiée : « SI le patient a une infection ET l'infection est bactérienne ET la bactérie est un streptocoque ALORS recommander la pénicilline ». Le moteur d'inférences utilisait un raisonnement basé sur cette base de connaissances et de règles et posait des questions au médecin pour l'aider à établir son diagnostic au fur et à mesure des réponses fournies par le médecin. En dépit de ses qualités, ce système expert n'a pas vraiment connu d'applications pratiques.

On comprend donc que l'enjeu de l'invention d'un système d'intelligence artificielle symbolique est de parvenir à trouver des heuristiques de pensées, qui permettent de déduire aussi rapidement que possible à partir d'une base de règles donnée, une et une seule réponse cohérente avec les données fournies.

Dans les années 1980, de nombreux systèmes dérivent de l'IA symbolique : la programmation logique, avec l'exemple du système PROGOL ; les arbres de décision, avec l'exemple connu de l'algorithme ID3 (acronyme de Iterative Dichotomiser 3) ; l'ingénierie des connaissances ou encore les ontologies^40(*) qui aboutiront dans les années 2000 au « Web sémantique »^41(*), proposition originale de Tim Berners-Lee, qui avait été en 1990 l'inventeur du World Wide Web (WWW, le Web), des URL, du protocole de communication HTTP et du langage informatique HTML, alors qu'il travaillait à l'organisation européenne pour la recherche nucléaire (Cern).

Les six modèles d'alignement d'IBM (alignment models) ont dominé le marché des modèles de langage, dans les années 1990 et 2000, notamment pour la traduction automatique. Ils reposaient sur des modèles d'IA symbolique, avant l'émergence des LLM modernes basés sur les réseaux de neurones, bien plus efficaces.

Les IA symboliques peuvent être particulièrement utiles pour capitaliser les savoirs au sein d'une organisation. Leurs applications en ingénierie des connaissances sont donc nombreuses. Qu'il s'agisse de systèmes de planification, de graphes, d'ontologies ou de réseaux sémantiques, les IA symboliques permettent de modéliser les connaissances d'une organisation ou d'un domaine spécifique de façon systématique.

c) Des limites sémiotiques qui les éloignent de l'intelligence

L'expérience de pensée imaginée par John Searle dans un article de la revue Behavioral and Brain Sciences en 1980 et connue sous le nom d'expérience de la « chambre chinoise » a démontré l'incapacité des IA symboliques à comprendre ce qu'elles font, n'assurant qu'une exécution mécanique d'instructions^42(*).

Le tableau ci-après décrit cette expérience riche d'enseignements quant aux limitations intrinsèques de ces systèmes d'IA.

Pourquoi l'IA symbolique n'est pas intelligente : l'expérience de la chambre chinoise

John Searle, dans cet article de 1980, montre qu'une personne qui n'a aucune connaissance du chinois, et qui serait enfermée dans une chambre, est parfaitement capable de communiquer par écrit en chinois à la condition que soit mis à sa disposition un manuel contenant l'ensemble des règles permettant de répondre à des phrases écrites en chinois.

Et bien que cette personne n'ait aucune compréhension de la signification des phrases en chinois qu'elle reçoit et qu'elle émet, elle donne l'illusion de comprendre en se contentant de suivre des règles données. Appliquer « bêtement » des règles syntaxiques, comme le font les ordinateurs avec l'IA symbolique, ne suffit donc pas à engendrer une véritable compréhension sémantique.

Searle prend alors ses distances avec l'idée au principe du test de Turing, selon laquelle un programme informatique peut être qualifié d'intelligent s'il est capable de communiquer avec un humain sans que ce dernier ne puisse réaliser qu'il s'agit d'une machine.

Pouvoir faire illusion en reproduisant une langue, sans avoir aucune conscience du contenu communiqué, n'est pas une preuve d'intelligence. La maîtrise du langage n'est pas qu'une manipulation de symboles, c'est aussi l'entendement des concepts, le fait de comprendre le sens de ce qu'on dit, d'avoir conscience du contenu.

Les programmes informatiques sont des systèmes formels dont la structure est syntaxique alors que l'intelligence humaine articule la syntaxe avec des contenus mentaux à caractère sémantique.

L'IA est donc encore très loin de l'esprit humain, seul capable de faire l'expérience subjective de la compréhension du monde des choses, du monde des mots et des relations qui unissent ces deux mondes.

Les IA symboliques sont bien affectées de limites sémiotiques : en effet, on sait depuis au moins le linguiste Ferdinand de Saussure, s'inspirant d'études millénaires en sanscrit ainsi que d'Héraclite^43(*), qu'un mot est interprété avec un signifiant (le symbole ou la représentation mentale de l'aspect matériel du signe), un signifié (le concept ou la représentation mentale du contenu associé au signe) et son référent, un objet (ou un ensemble d'objets) concret désigné par le signe. Comme l'expliquait Ferdinand de Saussure au début du XX^e siècle, le signe linguistique unit non pas tant un nom et une chose (le dénoté), non pas un mot et un objet, mais un concept (la connotation) et une image acoustique (le symbole), le signifié et le signifiant. Le structuralisme donnera à cette approche le nom de « triangle sémiotique ».

Or, l'IA symbolique ne dispose que du signifiant auquel elle associe éventuellement un objet mais elle est incapable de prendre en considération le signifié du mot, les concepts lui restent totalement étrangers, aussi, elle manipule les symboles sans avoir aucune idée de ce qu'ils sont, sans les comprendre pourrait-on dire. L'IA symbolique se heurte donc à trois principaux problèmes : les connaissances, puisqu'il faut être en mesure de décrire le monde pour l'utiliser, l'inférence, puisqu'il faut être capable de recueillir une expertise capable d'extraire des règles, enfin le contrôle, puisque les possibilités, si elles sont trop nombreuses, deviennent impossibles à déterminer.

L'IA connexionniste, avec ses méthodes statistiques qui se rapprochent de la logique inductive, peuvent donner l'impression de se rapprocher davantage de ce que nous appelons communément « compréhension », lorsque nous faisons des raisonnements basés sur l'induction, mais sous une forme purement probabiliste, en restant de simples programmes informatiques basés sur des mathématiques. De simples programmes mais pas des programmes simples comme nous allons le voir.

2. L'intelligence artificielle connexionniste

a) Cadre et définition de ces « superstatistiques »

(1) À l'origine de tous ces systèmes : les classifieurs linéaires

Contrairement à l'intelligence artificielle symbolique, déterministe, l'intelligence artificielle connexionniste ne se base pas sur des règles et de la logique qui seraient codées par le développeur dans des programmes informatiques mais sur des statistiques et de l'analyse probabiliste de données en fonction de variables aléatoires (qui forment des processus dits « stochastiques »).

On parle parfois de ces technologies connexionnistes comme de « superstatistiques », ce qui distingue le Machine Learning (apprentissage automatique) des IA symboliques vues précédemment. Elles sont ainsi qualifiées de par leur capacité à traiter de très grandes quantités de données via des méthodes statistiques complexes. Ce concept de superstatistiques appliqué à l'intelligence artificielle doit être distingué de celui relevant de la physique statistique^44(*).

L'intelligence artificielle connexionniste est, il est vrai, largement issue d'algorithmes de classement statistique, au premier rang desquels les classifieurs linéaires (pouvant eux-mêmes faire figure de sous-catégorie de l'analyse factorielle discriminante, qui peut d'ailleurs autant être descriptive que prédictive). Ces classifieurs ont pour rôle de classer des « objets », c'est-à-dire de les caractériser comme appartenant à des groupes - ou « classes » - déterminés. Un objet est un ensemble de variables numériques (pensons à une plante que l'on décrirait par l'existence ou non d'une tige, la longueur de la tige, la présence ou non d'épines, la présence ou non d'une fleur, le nombre de pétales, un codage pour la couleur des pétales, etc.). Lorsqu'il n'y a que deux classes (par exemple, on cherche à classer des fleurs en « rose » ou « marguerite »), le classifieur linéaire est un instrument très simple : il assigne un poids, un coefficient pondérateur, à chacune des variables de l'objet étudié, fait le produit correspondant puis additionne l'ensemble - il fait une combinaison linéaire des variables, d'où le nom de « classifieur linéaire » ; il applique ensuite à la somme ainsi calculée une « fonction de décision » qui détermine l'appartenance de l'objet à l'une ou l'autre classe ou la probabilité que l'objet appartienne à l'une ou l'autre classe. La plupart des problèmes supposant en fait l'existence de plus de deux classes, on combine plusieurs classifieurs linéaires pour faire de la classification multi-classes, notamment avec les méthodes dites « un-contre-un » et « un-contre-tous ». En tout état de cause, les poids mis en oeuvre par un classifieur sont appris à partir d'un jeu de données d'apprentissage étiquetées.

Ces algorithmes reposent sur des fonctions qui convertissent le produit scalaire de vecteurs dans la sortie désirée selon un vecteur de poids appris à partir d'un ensemble d'apprentissage étiqueté. Ils peuvent modéliser des probabilités conditionnelles (« classifieurs génératifs », comme la classification bayésienne naïve, à ne pas confondre avec l'IA générative) ou, en vue d'être plus précis, recourir à une méthode discriminante.

Les « réseaux de neurones artificiels » - synonyme de « réseaux de neurones formels » - sont un des systèmes d'IA connexionnistes les plus utilisés. Lorsque les réseaux sont organisés de manière stratifiée et que les calculs sont réalisés par plusieurs « couches » de neurones fonctionnant en cascade selon plusieurs niveaux de représentations, la sous-catégorie de l'IA que les réseaux de neurones forment prend le nom d'une sous-sous-catégorie appelée « Deep Learning » ou « apprentissage profond ».

(2) La pierre angulaire théorique : le théorème d'approximation universelle

Bien que ses succès soient en grande partie empiriques, le paradigme connexionniste de l'intelligence artificielle s'est progressivement doté d'un cadre théorique solide permettant de démontrer sa validité scientifique. Cette branche de l'IA se base ainsi sur le théorème d'approximation universelle, prouvant que les réseaux de neurones, à partir d'une seule couche cachée, peuvent approximer n'importe quelle fonction continue à la condition que la fonction d'activation soit non linéaire^45(*).

Ce théorème a été prouvé, dans un premier temps, par George Cybenko en 1989 pour certains modèles connexionnistes aux fonctions d'activation sigmoïdes^46(*). La même année, Kurt Hornik et son équipe ont démontré plus largement que les réseaux de neurones multicouches sont en réalité des approximateurs universels^47(*). D'autres chercheurs ont ensuite établi, ces dernières années, que cette propriété d'approximation universelle correspond à une fonction d'activation non polynomiale et ont étendu le théorème à d'autres fonctions et domaines^48(*). De ce fait, dès lors que leur architecture permet d'approximer suffisamment bien la fonction recherchée, les réseaux de neurones permettent de réaliser de nombreuses tâches de classification exigeantes.

b) Les réseaux de neurones artificiels : aux origines de l'apprentissage profond ou Deep Learning

(1) Les premières théories dans les années 1940

Dès 1943, le neurologue Warren McCulloch et le psychologue logicien Walter Pitts, travaillant tous les deux sur l'action des neurones dans le cerveau humain, mettent au point un modèle de « réseau de neurones » s'inspirant de l'anatomie animale et humaine^49(*). Les neurones humains sont à cette époque une découverte relativement récente, le terme n'apparaissant d'ailleurs qu'à la fin du XIX^e siècle grâce au développement du microscope optique.

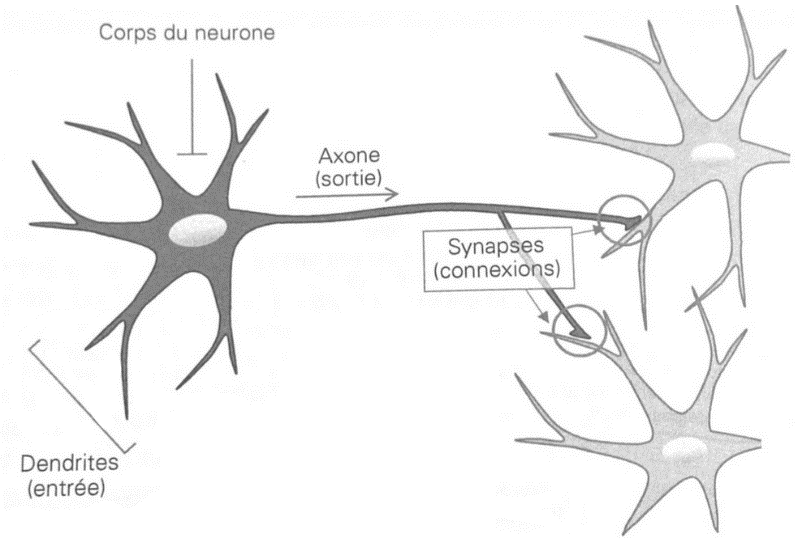
La structure des neurones est déjà connue dans la première moitié du XX^e siècle : des cellules nommées « neurones » transmettent une information à travers des axones, qui se lient aux entrées des autres neurones, appelées « dendrites » par le biais d'une connexion nommée « synapse ».

En revanche, la façon dont une telle structure était capable de transporter l'information restait totalement inconnue. C'est dans cette optique que les chercheurs ont d'abord voulu schématiser simplement le fonctionnement des réseaux de neurones humains, sans avoir pour but d'utiliser un tel modèle pour traiter efficacement de l'information, ni a fortiori pour faire progresser l'informatique et inventer l'IA.

Schéma simplifié d'un neurone biologique

Source : Jean-Paul Haton et al., 2023, Intelligences artificielles : de la théorie à la pratique. Modèles, applications et enjeux des IA, Dunod, p. 60

Les deux chercheurs ont alors imaginé la transposition d'une telle configuration dans un mode purement formel, en s'inspirant des portes logiques en mathématiques.

L'idée est donc qu'un « neurone » artificiel ou formel pourrait accueillir des entrées provenant de neurones d'une couche précédente. Ce « neurone » ferait alors, tel un automate, la somme des entrées de la couche précédente, une somme qui serait pondérée par des « poids » (ces poids miment la plasticité synaptique des réseaux biologiques). Cette somme serait alors soumise à une fonction d'activation non linéaire qui, agissant comme un seuil franchi ou non, détermine si le neurone active ou non sa sortie - l'application de cette fonction à la somme des valeurs issues des entrées des couches précédentes permettant ou pas d'atteindre une valeur seuil donnée.

Dans leur article de 1943, McCulloch et Pitts affirment que de tels réseaux pourraient effectuer des calculs logiques. Ainsi, ils conçoivent des « portes logiques », c'est-à-dire des opérateurs dont les entrées et les sorties reposent sur la logique booléenne (seules deux valeurs sont possibles, qu'on représente en général par les couples « vrai / faux » ou « 1 / 0 »).

On est encore loin des réseaux de neurones qui seront utilisés plus tard pour développer l'intelligence artificielle connexionniste telle que nous la connaissons mais les auteurs ouvrent un nouveau champ de travail.

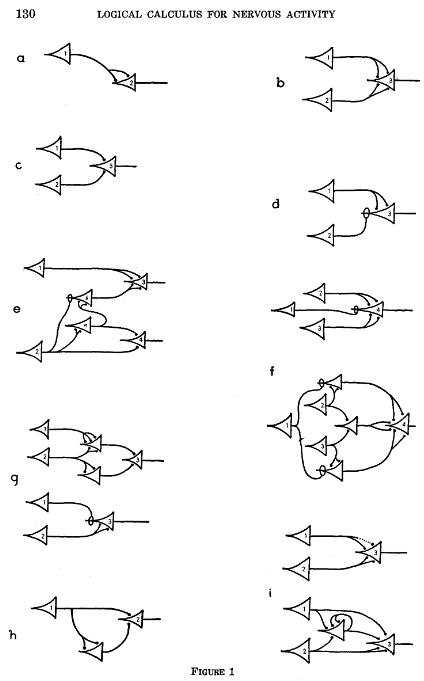
Le schéma suivant présente les fonctions logiques que McCulloch et Pitts ont mises au point grâce à leur schématisation des réseaux de neurones, les triangles y représentant les neurones et les flèches y renvoyant aux connexions synaptiques.

Fonctions logiques selon les réseaux schématiques de neurones définis par McCulloch et Pitts en 1943

Source : McCulloch et Pitts, « A logical calculus of the ideas immanent in nervous activity », op. cit.

Les travaux de McCulloch et Pitts dans les années 1940 ne sont que théoriques, ils n'ont pas, à l'époque, l'idée de réaliser physiquement de tels réseaux de neurones artificiels, encore moins de les simuler via un programme informatique. Leur objectif est notamment de décrypter le fonctionnement des neurones responsables de la vision chez les humains et les animaux. C'est néanmoins sur la base de ces schémas de neurones formels interconnectés en portes logiques que vont s'appuyer les travaux postérieurs en mathématiques et en informatique pour développer progressivement les réseaux de neurones artificiels.

En 1959, McCulloch et Pitts, aidés de Lettvin et Maturana, se demandent « ce que l'oeil d'une grenouille dit à son cerveau » et précisent la transposition imaginée en 1943 avec un modèle simplifié de neurone biologique appelé neurone formel^50(*). Ces neurones formels associés en réseau comparent la somme de leurs entrées et, si une valeur seuil est atteinte, répondent en émettant un signal. Ces réseaux reposent donc sur des fonctions de transfert. Et comme dans le cas des réseaux de neurones biologiques, il est imaginé que la force de connexion entre les neurones - l'efficacité de la transmission des signaux d'un neurone à l'autre - peut varier. Pour autant les auteurs ne présentent pas encore un système artificiel capable d'apprendre par l'expérience. C'est un autre chercheur qui va théoriser, sous le nom de « perceptron », les algorithmes d'apprentissage permettant de faire varier la force de connexion entre les neurones artificiels. Avec les perceptrons, le poids synaptique au sein des neurones formels va se trouver modifié et amélioré selon des processus d'apprentissage.

(2) Les premiers perceptrons

(a) Les perceptrons monocouches

La première apparition d'un modèle pouvant être considéré comme l'ancêtre des réseaux de neurones artificiels actuels plutôt que comme une simple source d'inspiration théorique est le perceptron monocouche, inventé au laboratoire d'aéronautique de l'université Cornell par le psychologue Frank Rosenblatt en 1957 et ayant conduit à une publication en 1958^51(*). Il permet le classement binaire linéaire supervisé d'une population, c'est-à-dire un processus permettant de séparer une population en deux classes, en connaissant déjà la classe d'une partie des individus. On retrouve ici le principe du classifieur linéaire évoqué dans les développements précédents. Ce réseau est capable d'apprentissage : là où les poids synaptiques sont figés dans les réseaux de McCulloch et Pitts, le perceptron, lui, peut faire varier ses poids grâce à une règle d'apprentissage du perceptron, appelée aussi « loi de Widrow-Hoff » ou filtre des moindres carrés moyens (Least Mean Squares ou LMS).

Le perceptron monocouche est composé de plusieurs entrées et d'une seule sortie (booléenne) à laquelle toutes les entrées (booléennes) sont connectées. Il est utilisé pour résoudre des problèmes de classification linéaire, c'est-à-dire des problèmes qui peuvent être résolus en séparant deux classes d'une population par une droite ou un plan, que l'on qualifie spécifiquement d'hyperplan dans le cadre des réseaux de neurones^52(*).

Prenons l'exemple d'une population dont on connaît la taille et le poids et dont on souhaite classer les individus par genre. Les caractéristiques de la population sont deux variables continues « taille » et « poids » et les deux classes auxquelles les individus peuvent appartenir sont « homme » ou « femme ». On peut représenter les individus par des points situés sur un graphique en deux dimensions qui aurait pour abscisse la taille des individus et pour ordonnée leur poids. Les hommes étant généralement plus grands et massifs que les femmes, le graphique fait apparaître deux groupes de points qui représentent respectivement les hommes et les femmes et sont à peu près séparés l'un de l'autre. L'apprentissage va consister à déterminer la droite qui sépare « le mieux possible » le groupe des points représentant les hommes et celui des points représentant les femmes, pour le jeu de données d'apprentissage choisi (c'est-à-dire un ensemble d'individus dont on connaît la taille et le poids, et dont chacun dispose de son étiquette « homme » ou « femme »). Dès lors on pourra déterminer la classe probable d'un nouvel individu (en l'occurrence son genre) en connaissant son poids et sa taille, selon que le point qui le représente sur le graphique sera placé d'un côté ou de l'autre de la droite séparatrice.

Pour passer du langage géométrique au langage algébrique pertinent pour le perceptron :

· la droite séparatrice est entièrement déterminée par son équation cartésienne, concrètement trois nombres

 : elle est l'ensemble des points du plan dont les coordonnées (taille, poids) vérifient

· le perceptron est un opérateur qui, pour tout individu, calcule la quantité

· les coefficients ₁ et ₂ sont les « poids synaptiques » qui pondèrent les valeurs reçues aux entrées du perceptron ; le coefficient b est appelé un « biais » du perceptron

· selon que le résultat Y est positif ou négatif, l'individu est un homme ou une femme ; si Y est nul, l'individu ne peut être classé.

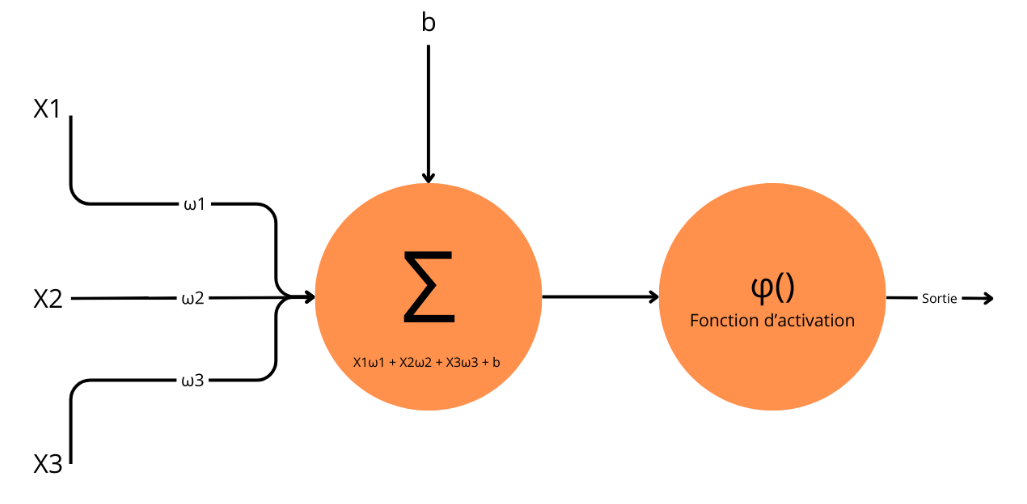
Le schéma ci-après illustre un perceptron qui traite trois variables en entrée et dont le résultat Y est soumis à une fonction d'activation, pour transmission éventuelle au perceptron suivant. Le principe est évidemment généralisable à un nombre supérieur de variables.

Schéma d'un perceptron monocouche avec fonction d'activation

Le perceptron dispose donc de la capacité de séparer une population en deux classes dont la « frontière » dépend des poids synaptiques

. Toutefois, il manque toujours à ce réseau un système d'apprentissage qui lui permettra de déterminer les poids synaptiques grâce auxquels la population sera séparée de façon optimale. Pour cela, on utilise la loi de Widrow-Hoff.

Le principe consiste à soumettre au perceptron une série d'individus d'entraînement. On détermine l'écart entre le résultat Y calculé par le perceptron pour le premier individu et le résultat Y attendu ; les poids synaptiques sont alors ajustés en fonction de cet écart ; on réitère le processus en soumettant au perceptron successivement tous les individus d'entraînement, jusqu'à ce qu'il n'y en ait plus ou que le nombre d'erreurs du perceptron soit devenu acceptable.

Pour que ce processus d'entraînement fonctionne, il faut fixer ce que l'on appelle un « hyperparamètre », c'est-à-dire un paramètre qui affecte le comportement d'un modèle et qui est choisi par son concepteur pour son entraînement. Dans le cas de la loi de Widrow-Hoff, l'hyperparamètre est un « taux d'apprentissage », qui détermine l'importance de l'ajustement apporté aux poids synaptiques lorsqu'on soumet un individu d'entraînement au perceptron. Une valeur élevée du taux d'apprentissage favorise un apprentissage rapide mais expose à l'apparition d'erreurs plus fréquentes ; au contraire, un taux d'apprentissage faible réduit le risque d'erreur mais ralentit le processus d'apprentissage.

En 1982, le physicien John Hopfield cherche à enrichir les réseaux de neurones artificiels de la rigueur propre aux physiciens et ouvre la voie aux modèles dits à base d'énergie : la dynamique du réseau est à temps discret et asynchrone, ce qui signifie qu'un seul neurone est mis à jour à chaque unité de temps^53(*). Ces modèles de réseaux de neurones dits de Hopfield vont rapidement se généraliser et actualiser la grande majorité des nouveaux perceptrons.

Bien que le perceptron constitue une avancée importante dans le développement de l'IA connexionniste, son intérêt reste alors limité : il ne peut effectuer que des séparations linéaires. Ce type de séparation, bien que permettant certaines classifications, ne correspond pas à la majorité des cas réels, où les classes d'une population donnée sont séparées par des fonctions plus complexes qu'une simple fonction linéaire. Par exemple, ces premiers perceptrons ne sont pas capables de résoudre des problèmes non linéaires comme la disjonction exclusive ou fonction « ou exclusif » (appelée aussi XOR, connue en électricité sous la forme du montage va-et-vient et utilisée en cryptographie, à l'instar du « téléphone rouge » entre la Maison-Blanche et le Kremlin dans les années 1970 et 1980).

Pour résoudre des problèmes non linéaires, une seule couche de réseaux de neurones n'est pas suffisante : plusieurs couches de réseaux de neurones vont alors être utilisées. On parle donc de « perceptron multicouche » (multilayer perceptron, ou MLP). Ces perceptrons multicouches ont tout d'abord pris la forme de « réseaux de neurones à propagation avant » ou « réseaux de neurones à action directe » (en anglais feedforward neural networks (FNN).

(b) Les perceptrons multicouches (MLP) et les réseaux de neurones à propagation avant (FNN)

Dans le livre Perceptrons : une introduction à la géométrie informatique, de Marvin Minsky et Seymour Papert publié en 1969, les deux auteurs estiment qu'imiter le cerveau est trop complexe pour des machines et démontrent l'incapacité des perceptrons monocouches à résoudre des problèmes de classification non linéaires^54(*). Ce livre, pessimiste, est accusé d'être à l'origine d'un premier « Hiver » de l'intelligence artificielle.

La sortie de ce livre est en effet corrélée avec une période de relative accalmie dans le développement et le financement de l'intelligence artificielle et par un quasi-abandon des perceptrons et plus généralement des réseaux de neurones artificiels^55(*). Elle n'est pas pour autant la seule raison de ce ralentissement : les limitations des technologies alors disponibles, les données en nombre insuffisant et le manque de puissance de calcul sont les trois facteurs principaux. La recherche autour de l'intelligence artificielle connexionniste a été ranimée dans les années 1980 par les réseaux de Hopfield et surtout par les MLP.

On parle de perceptrons multicouches lorsque le réseau de neurones est composé de perceptrons organisés en plusieurs couches. Lorsque l'information n'y circule que dans un sens, de l'entrée vers la sortie, on a affaire à des « réseaux de neurones à propagation avant » (en anglais feedforward neural network, FNN), pour les distinguer des réseaux de neurones récurrents (RNN), où l'information effectue au moins un cycle dans la structure du réseau (ces réseaux plus complexes seront vus plus loin).

Dans les MLP, chaque couche agit de la même façon qu'un perceptron classique, et les différentes couches sont montées « en série ». La première couche est appelée couche d'entrée. C'est ici que sont introduites les données que l'on veut traiter. La couche d'entrée transforme ces données en données numériques pour qu'elles puissent être traitées par le réseau.

Ensuite, il y a une ou plusieurs couches cachées. Chaque couche est composée de neurones, et chaque neurone a une ou plusieurs entrées et sorties. Ces entrées et ces sorties forment des ensembles fonctionnels qui se comportent chacun comme des perceptrons. Ils associent à une valeur des coefficients (les poids synaptiques) et un biais. Comme pour le perceptron monocouche, chaque entrée reçoit une valeur de la couche précédente. Cette valeur est multipliée par un autre élément appelé « poids synaptique », qui définit la force du lien entre deux neurones. Si un neurone a plusieurs entrées, toutes les valeurs sont additionnées, et on ajoute une autre valeur pour chaque neurone appelé « biais ». De la même façon que pour un perceptron monocouche, cette somme est ensuite passée dans une fonction d'activation, qui décide si la sortie doit être activée ou non. Il existe différentes fonctions d'activation, comme la fonction « marche » ou la fonction « unité de rectification linéaire » dite ReLU. Le résultat de la fonction est la sortie du neurone, et devient une entrée pour la couche suivante.

Enfin, il y a la couche de sortie, qui, de la même façon qu'un perceptron monocouche, transforme les valeurs obtenues en réponse au problème posé. Par exemple, si l'on souhaite savoir s'il s'agit d'un chat ou un chien sur une image, la couche de sortie donne la réponse grâce à un neurone correspondant à la probabilité qu'il y ait un chien sur l'image et un autre neurone correspondant à la probabilité qu'il y ait un chat sur l'image.

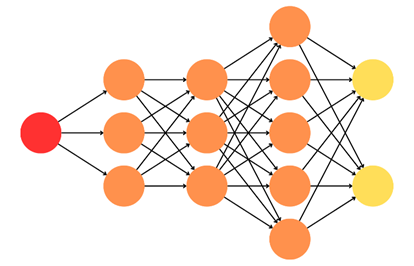
Schéma d'un perceptron multicouche

Légende : la couche d'entrée est en rouge, les couches cachées en orange et la couche de sortie en jaune

Ce schéma permet de voir concrètement les trois couches qui composent le modèle. À gauche, on a une couche d'entrée, ici constituée d'un neurone unique mais en fonction du type de données en entrée, on pourrait en avoir plusieurs. Au milieu, on a les couches cachées. Ici il y en a trois, il pourrait y en avoir plus : ce paramètre entre en jeu dans l'élaboration d'un modèle efficace, aussi économique et fiable que possible. Chaque couche n'est pas obligée de contenir le même nombre de neurones : dans l'exemple, les deux premières couches contiennent trois neurones, la troisième en contient cinq. Puisque dans cet exemple tous les neurones d'une couche sont reliés à tous les neurones de la couche suivante, on parle de « réseau dense ». À droite, enfin, on a la couche de sortie, qui contient ici deux neurones mais qui pourrait en contenir plus ou moins en fonction du type de données que l'on veut en sortie.

Tableau non exhaustif de fonctions d'activation couramment utilisées

Nom de la fonction	Équation associée	Représentation graphique
Identité
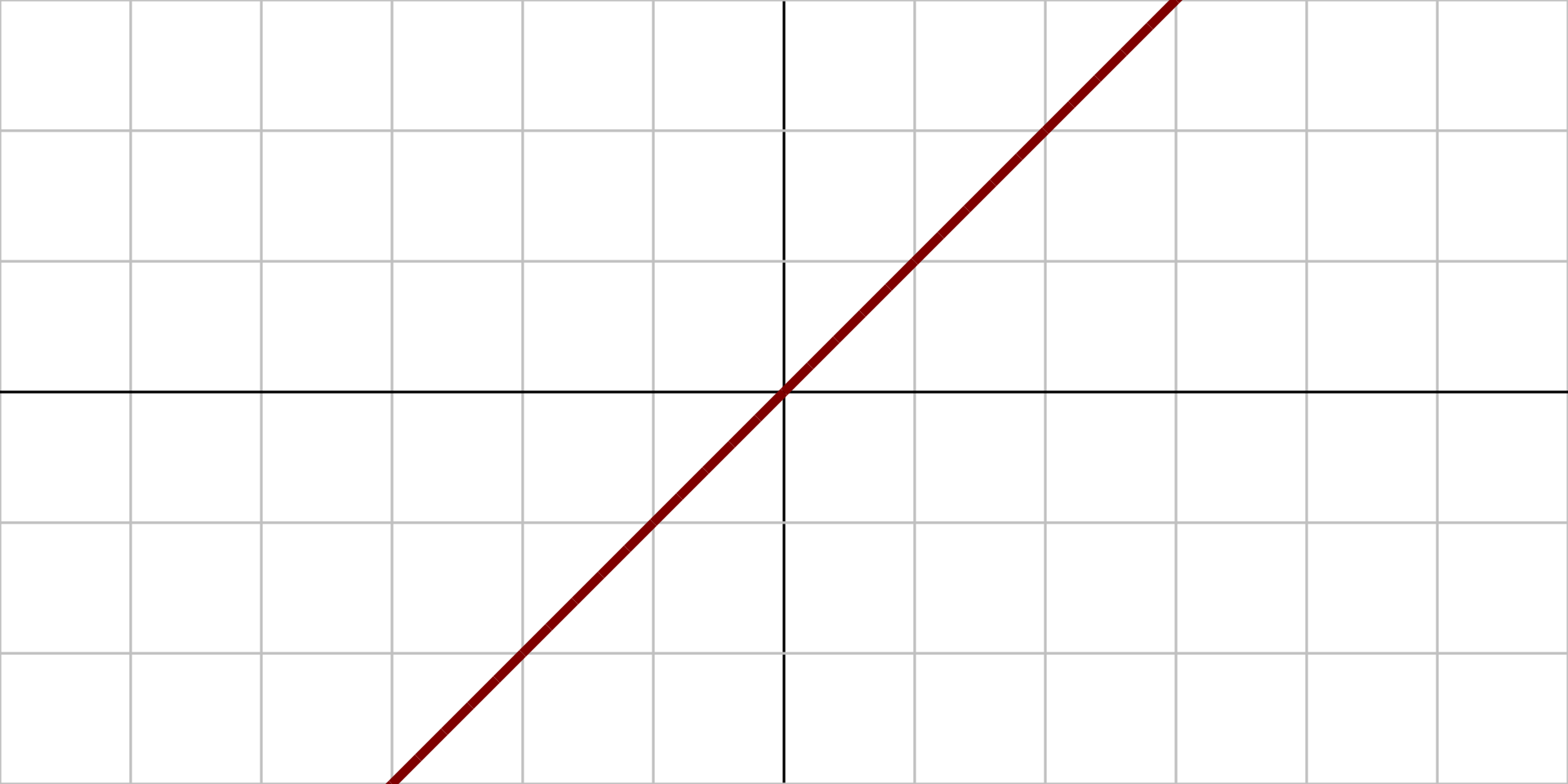
Marche
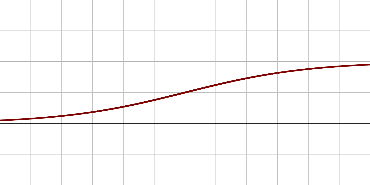
Sigmoïde
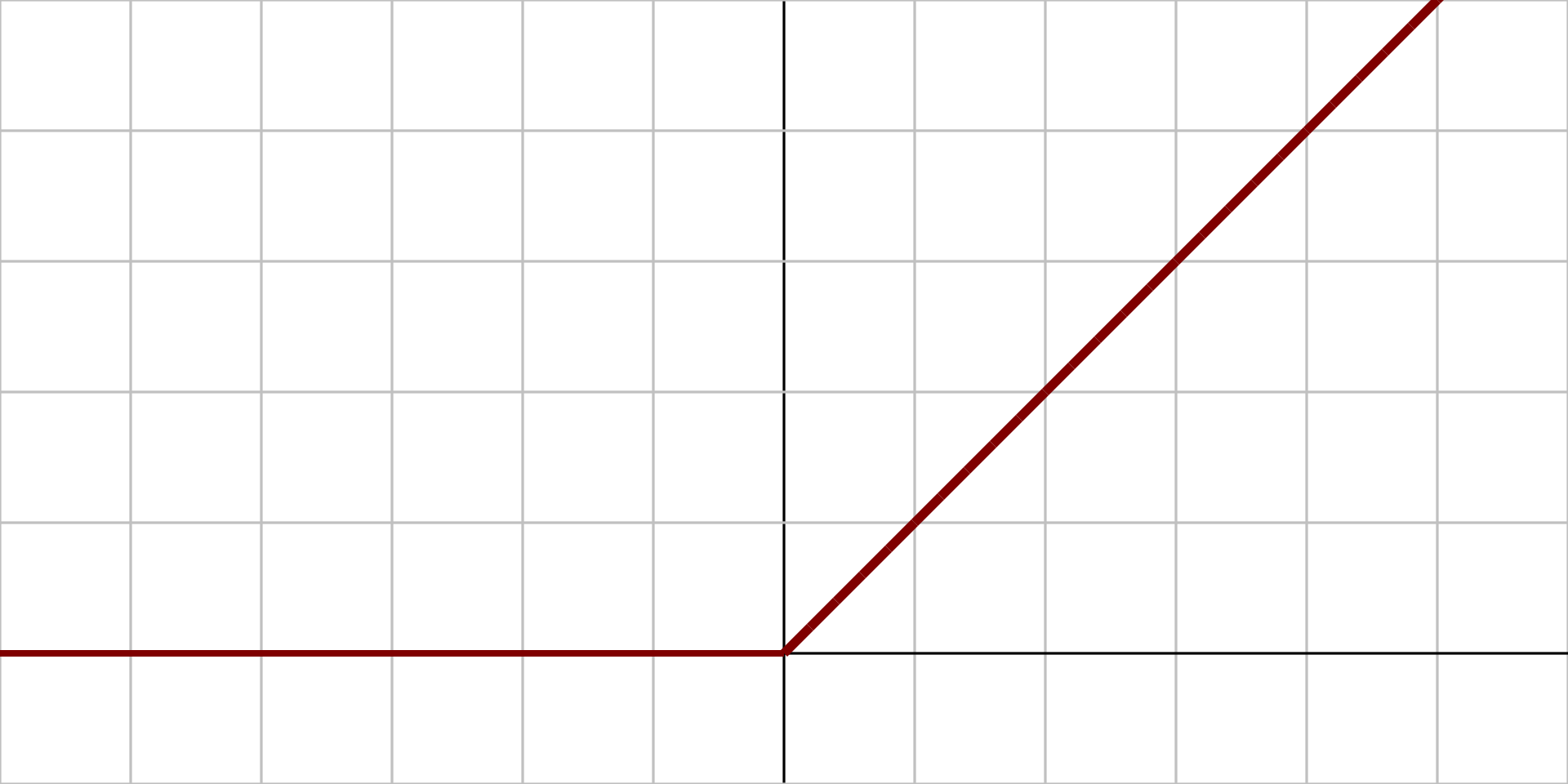
Unité de rectification linéaire (ReLU)
Unité de rectification linéaire douce (SoftPlus)
Sinus cardinal

Source : Exemples pris parmi la liste des 16 fonctions d'activation usuelles recensées par Wikipédia

Il est possible de prendre l'exemple concret d'un réseau multicouche simple pour expliquer le fonctionnement de ces réseaux de neurones artificiels.

Ce modèle d'illustration est inventé afin de permettre une compréhension plus aisée du concept. Les réseaux de neurones sont, en effet, beaucoup plus grands, et les informations traitées bien plus nombreuses (plusieurs milliards). Le chemin de l'information va de l'entrée du modèle vers sa sortie.

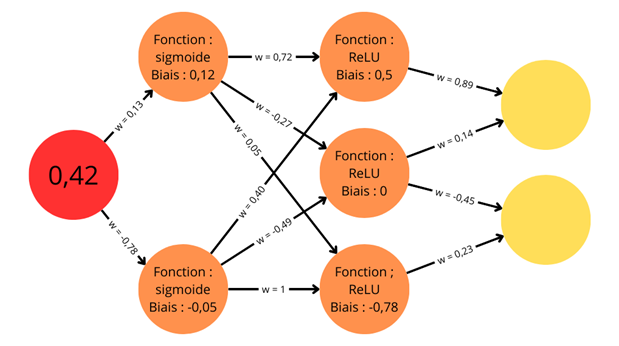
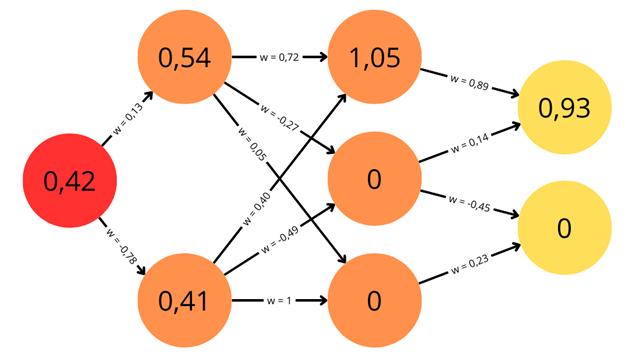
Exemple de schéma d'un réseau de neurones avec des valeurs associées aux synapses (poids, noté w) et aux neurones (biais)

Sur ce schéma sont présentées toutes les informations qui permettent de calculer des valeurs de sorties dans les neurones de la couche de sortie. On dispose d'une valeur d'entrée dans le neurone d'entrée : 0,42. À chaque synapse est associé un poids synaptique noté « w ». Pour chaque couche de neurones cachés, on a une fonction d'activation : sigmoïde pour la première, ReLU pour la seconde. À chaque neurone est associé un biais.

Le calcul pour les deux neurones de la couche cachée peut être détaillé. Pour cela, la valeur initiale est multipliée par le poids synaptique de la synapse qui la relie au neurone dont on veut connaître la valeur, et on y ajoute le biais. On a donc :

et

Ces valeurs passent ensuite dans la couche d'activation afin d'obtenir le poids final de chaque neurone. On calcule donc la valeur de la fonction sigmoïde pour

et

. On obtient 0,54 pour le premier neurone et 0,41 pour le second neurone. La seconde couche de neurones ayant une valeur, on peut alors calculer grâce à celle-ci la troisième couche comme on l'a fait avec la première. Tous les neurones de la deuxième couche étant reliés à tous les neurones de la troisième couche, le calcul est un peu plus complexe puisqu'il faut additionner les valeurs des entrées avant de les faire passer dans la fonction d'activation.

On a alors :

Ces valeurs peuvent alors passer dans la fonction d'activation ReLU. On obtient donc les poids des trois synapses de la couche suivante : 1,05 ; 0 et 0 (lorsque les nombres sont négatifs, la fonction ReLU renvoie toujours 0).

Enfin, les poids des neurones de la couche de sortie sont calculés :

Le schéma initial du réseau de neurones peut être complété avec toutes les valeurs qui viennent d'être calculées.

Schéma complété des calculs réalisés

On a donc un résultat dans la couche de sortie qui nous permet d'interpréter ce que le modèle a pu discriminer. En réalité, ces calculs ne sont jamais effectués manuellement et un ordinateur peut réaliser tous ces calculs beaucoup plus rapidement qu'un humain pour en tirer des résultats beaucoup plus précis car gardant le plus de chiffres possible après la virgule dans les calculs.

C'est la multiplication des couches de perceptrons qui a conduit à parler d'apprentissage profond ou Deep Learning. Ce type de réseau découle du perceptron monocouche imaginé par Rosenblatt lors de ses travaux. L'idée de mettre des perceptrons en couches successives ne constitue cependant pas l'avancée majeure des MLP par rapport aux perceptrons monocouches. Ces perceptrons multicouches à propagation avant ou FNN présentent en effet un désavantage par rapport à un perceptron monocouche. Bien que les réseaux à plusieurs couches soient capables de traiter des situations de classification non linéaire, avec plusieurs neurones au lieu d'un seul, il n'est plus possible de calculer la façon dont on doit entraîner le réseau pour qu'il produise de meilleurs résultats. Là où l'on utilisait la loi Widrow-Hoff pour le perceptron monocouche, il n'est plus possible de le faire désormais car il y a plusieurs neurones dont les paramètres influencent le résultat final d'une façon différente. Comment alors savoir quel poids synaptique ou quel biais modifier et de quelle façon pour atteindre le résultat optimal voulu ? L'incapacité à répondre à de telles questions est l'une des raisons de « l'Hiver » de l'IA des années 1970. En effet, ces réseaux FNN ne présentent pas d'intérêt s'ils ne sont pas capables de répondre à ces questions puisque leur intérêt était précisément d'être capables « d'apprendre », c'est-à-dire d'adapter leurs réponses.

Des scientifiques commencent à répondre à cette difficulté dans les années 1980 en utilisant une technique issue de la résolution des problèmes de fonctions convexes en mathématiques appelée la « descente de gradient ». L'algorithme permettant de trouver un minimum global, c'est-à-dire le point où le modèle obtient les meilleurs résultats, va prendre le nom de rétropropagation du gradient, permettant alors d'utiliser les perceptrons multicouches (MLP) de façon optimale et quasi automatisée.

(3) La rétropropagation du gradient (Back-propagation)

Les méthodes algorithmiques visant à corriger les erreurs des MLP et à les améliorer sont issues du calcul de la descente du gradient et sont appelées algorithmes de rétropropagation du gradient ou de rétropropagation des erreurs. Elles se fondent sur les travaux de Seppo Linnainmaa, qui décrit de tels algorithmes dès son mémoire de maîtrise en 1970 mais sans les appliquer aux réseaux de neurones. Paul Werbos imagine dans sa thèse de doctorat en 1974 de nouveaux outils de prévision qui appliqueraient la rétropropagation du gradient aux réseaux de neurones. Ces premiers travaux ne conduisent pas à des résultats concrets. On considère en effet que le premier perceptron multicouche efficace date de 1986.

Pour régler les perceptrons multicouches, c'est-à-dire minimiser leur taux d'erreur, la descente du gradient doit conduire à ajuster progressivement le poids de tous les neurones au sein du modèle. Un collectif de chercheurs (Hinton, Rumelhart, Williams et McClelland) élabore alors un algorithme de descente du gradient qui va prendre le nom de rétropropagation du gradient^56(*) : il s'agit de parcourir le réseau de neurones dans le sens inverse de son fonctionnement pour corriger ses erreurs en mettant à jour par cet algorithme les poids des neurones de la dernière couche à la première.

De jeunes chercheurs comme Yann LeCun et Yoshua Bengio, rencontrés par vos rapporteurs, ont alors poursuivi à partir du milieu des années 1980 des recherches sur ces nouvelles architectures^57(*). En 2019, Geoffrey Hinton, Yann LeCun et Yoshua Bengio ont reçu le prestigieux prix Turing pour l'ensemble de ces travaux fondateurs pour les architectures modernes des réseaux de neurones profonds (ce prix est l'équivalent pour l'informatique du prix Nobel ou de la médaille Fields, récompense la plus prestigieuse de la discipline mathématique).

Il est intéressant de relever qu'un phénomène biologique similaire à la rétropropagation du gradient a été observé dans les réseaux de neurones des mammifères^58(*).

Un des intérêts des réseaux de neurones multicouches est que le modèle évolue grâce à un entraînement qui lui permet d'être de plus en plus performant. Celui-ci consiste, en utilisant un jeu de données d'entraînement, à mesurer l'écart entre la réponse fournie par le modèle et la réponse attendue, et à ajuster le modèle pour minimiser cet écart.

S'agissant du premier point, l'écart entre le résultat effectif et le résultat attendu peut se calculer de différentes façons. La plus simple consiste peut se calculer de différentes façons. La façon la plus simple revient à calculer l'« erreur quadratique moyenne » (mean square error, MSE), c'est-à-dire la différence entre la donnée de sortie du modèle et la donnée attendue au carré, permettant d'obtenir une « fonction de perte » ou « fonction de coût ». Si l'on prend l'exemple d'un modèle qui doit déterminer si une image est, ou non, celle d'un chat, et que l'on introduit une image de chat dans le modèle puis que celui-ci donne 0,8 en sortie, la perte sera de

. En effet, la sortie attendue était 1 (car l'image est bien celle d'un chat).

Pour ce qui concerne le second point, l'ajustement consiste à « surfer » sur la fonction de perte pour descendre vers son minimum, en faisant varier les poids et les biais des neurones. À cette fin, on détermine la façon dont de petites variations de chaque poids ou biais, réalisées séparément, font varier la fonction de perte ; ceci revient, en mathématiques, à calculer les dérivées partielles de la fonction de perte par rapport à chaque poids ou biais. Le vecteur contenant l'ensemble des valeurs de ces dérivées est appelé le gradient.

Pour régler les poids et biais des neurones, on commence à travailler sur la fonction de perte à partir des neurones de la dernière couche. Un algorithme - dit optimiseur - est appliqué au gradient pour le « descendre » en ajustant les poids et les biais dans la direction opposée au gradient. Chaque poids et biais de chaque neurone reçoit une correction qui fait intervenir la dérivée partielle correspondante de la fonction de perte et un taux d'apprentissage. Le choix de l'optimiseur dépend de la nature des données traitées et de la rapidité (souhaitée et possible) de la convergence vers la perte minimale ; il en existe un grand nombre : descente de gradient stochastique (stochastic gradient descent ou SGD), Adagrad, Adadelta, RMSprop, Adam... La rétropropagation proprement dite consiste à réaliser ensuite les mêmes opérations aux neurones de la couche située immédiatement en amont, puis de la précédente, etc. De cette façon, toutes les couches du modèle sont remontées une par une, depuis la couche de sortie jusqu'à la couche d'entrée.

Cette méthode de rétropropagation du gradient a suscité un regain d'intérêt pour les réseaux de neurones sous leur nouvelle forme d'apprentissage profond, et donc pour l'ensemble du paradigme connexionniste. Au-delà du prix Turing décerné en 2019 à trois de ses inventeurs - Geoffrey Hinton, Yann LeCun et Yoshua Bengio^59(*) - c'est le prix Nobel de physique qui récompense en 2024 Geoffrey Hinton et John Hopfield pour leurs travaux sur les réseaux de neurones artificiels.

(4) Les réseaux de neurones convolutifs (CNN)

Un réseau de neurones artificiels traite en entrée des données numériques et délivre en sortie d'autres données numériques. Pour mettre en oeuvre de tels modèles, il faut donc pouvoir transformer l'information que l'on veut traiter en données numériques, en perdant le moins de sens possible. Dans le cas d'une image en couleur, il s'agit d'identifier les formes, les contrastes, éventuellement les ombres, etc. Les chercheurs ont dû inventer des réseaux permettant de conserver ces informations et de les convertir en données numériques pour qu'elles soient traitées par un réseau, capable de réaliser par exemple des tâches de classification.

Les réseaux convolutifs (convolutional neural networks ou CNN) sont ainsi des réseaux de neurones utilisés pour le traitement des images. Tout comme les travaux sur les perceptrons, ces réseaux de neurones sont influencés par des avancées scientifiques, notamment dans les sciences cognitives. Les travaux de Hubel et Wiesel en 1968 sur les cellules visuelles dans le cerveau des animaux^60(*), qui leur a valu un prix Nobel de physiologie en 1981, ont inspiré les informaticiens sur la façon dont il était possible de traiter une information visuelle grâce à un réseau de neurones situés dans le « cortex strié » (ou cortex visuel primaire). Hubel et Wiesel ont également découvert qu'il existait deux types de cellules dans ce cortex, une partie de ces neurones ne traitant l'information que d'une partie de l'image perçue par les capteurs visuels.

C'est cette idée qui a inspiré le scientifique japonais Kunihiko Fukushima lors de la création de deux modèles : le cognitron en 1975^61(*) puis le neocognitron en 1980^62(*). Ces réseaux, imitant le fonctionnement du cerveau, ne sont pas encore des réseaux convolutifs mais s'en rapprochent et sont souvent considérés comme les réseaux qui ont permis l'émergence des CNN.

Yann LeCun écrit : « Les cellules simples du Néocognitron sont un bricolage byzantin pour coller au mieux à la biologie et faire en sorte que le réseau fonctionne. [...] Peut-être Fukushima veut-il imiter trop étroitement la biologie ? Toujours est-il que le résultat est moyennement heureux. »^63(*)

L'un des premiers réseaux convolutifs à recevoir un usage pratique s'appelle « LeNet-5 » et est développé notamment par Yann LeCun et Yoshua Bengio dans l'entreprise Bell Labs en 1989^64(*). L'objectif du modèle était alors de reconnaître automatiquement les codes postaux manuscrits. Il sera largement utilisé.

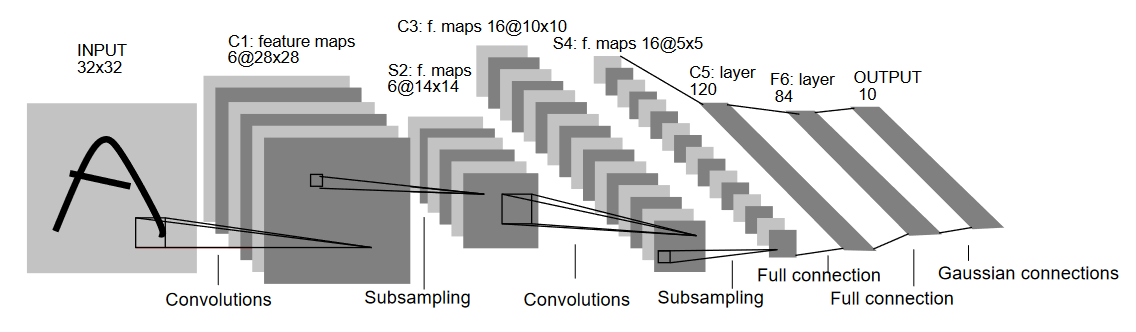
Schéma du réseau de convolution LeNet-5

Source : LeCun et al., 1989

LeNet est le premier réseau convolutif à présenter cette architecture toujours utilisée à l'époque actuelle dans les réseaux convolutifs comme les réseaux ResNet^65(*). On voit sur le schéma qu'il est constitué d'une succession de couches de « convolution » et de « sous-échantillonnage » (subsampling). L'objectif est de réaliser un « encodage » de l'image d'entrée, afin d'en extraire les caractéristiques importantes.

Pour obtenir des valeurs numériques à partir d'une image, on attribue des valeurs à chacun de ses pixels. Dans le cas d'une image en niveaux de gris (noir et blanc), chaque pixel a une valeur, qui va de zéro, totalement noir, à un, totalement blanc. Dans le cas d'une image en couleur, chaque pixel est composé d'un vecteur de trois valeurs. En effet, une image en couleur peut être représentée comme une superposition de la même image respectivement en rouge, vert et bleu (on parle de système RVB ou RGB pour red green blue en anglais). Ces couleurs étant les couleurs primaires de la lumière, on peut obtenir l'importe quelle couleur à partir d'un mélange de ces trois couleurs. Par exemple, le jaune étant un mélange de rouge et vert, un pixel jaune sera représenté par le vecteur (1, 1, 0), c'est-à-dire tout à fait rouge et tout à fait vert sans bleu. Les valeurs RGB s'exprimant généralement jusqu'à 255, on normalise ces valeurs dans les modèles pour qu'elles soient contenues entre zéro et un ; les valeurs sont donc divisées par 255.

Dans un CNN, l'objectif est de réduire les dimensions de l'image en gardant ses principales caractéristiques grâce à une opération mathématique appelée la « convolution ». Cette opération permet d'extraire des caractéristiques d'une image en faisant passer une « matrice de convolution » (kernel), qui réalise des opérations sur une zone de l'image, permettant de générer une « carte de caractéristiques » (activation map). On peut voir l'opération de convolution comme un tampon qui passerait au-dessus de chaque groupe de pixels dans une image et qui transformerait la valeur de ces pixels en fonction du tampon choisi.

On réalise cette opération plusieurs fois sur chaque couche d'une image (une couche ne pouvant être composée que d'un canal de couleur rouge, verte ou bleue) en changeant la matrice de convolution pour obtenir une série de cartes de caractéristiques de mêmes dimensions que l'image originale. Pour que le processus ne soit pas linéaire, on peut ajouter, après chaque couche de convolution, une fonction d'activation (souvent la fonction sigmoïde ou unité linéaire rectifiée, ReLU), cette fonction va prendre en entrée les cartes de caractéristique obtenues après application d'une convolution. Elle va renvoyer une valeur de sortie selon la fonction choisie^66(*).

L'objectif étant de réduire les dimensions de l'image, on applique une couche dite de max pooling (en français plus rarement : sous-échantillonnage par valeur maximale). Cette étape consiste à appliquer un filtre d'une taille définie sur une surface (en l'occurrence, sur les cartes de caractéristiques), et ne garder que la valeur maximale de la région définie par le filtre. Ainsi par exemple, un max pooling de 2x2 va parcourir les cartes de caractéristiques avec un filtre de deux pixels par deux, et sélectionner dans ce carré la valeur la plus importante. Cela permet de diviser la dimension des surfaces par deux. C'est ce qui est appelé la phase de sous-échantillonnage (subsampling).

Cette combinaison de convolution et max pooling est répétée sur les cartes de caractéristiques jusqu'à ce que l'on obtienne des dimensions suffisamment réduites. On réalise ensuite un « aplatissement » (flattening) des dimensions obtenues pour les stocker dans un vecteur à une seule dimension. Ce vecteur à une seule dimension est alors présenté à l'entrée d'un réseau dense de neurones, c'est-à-dire un réseau dont l'ensemble des neurones d'une couche sont reliés à l'ensemble des neurones de la couche précédente.

Ce réseau dense, qui fonctionne exactement comme un FNN, avec une couche de sortie construite selon le résultat souhaité.

Pour illustrer le fonctionnement d'un CNN, on peut imaginer utiliser en entrée une image carrée de dimension

(soixante-quatre pixels de longueur et de largeur, trois canaux de couleurs) afin de reconnaître un chiffre entre zéro et neuf. Cette image passe ensuite dans une couche de convolution qui va, par exemple, produire trente-deux cartes de caractéristiques en utilisant des matrices de convolution différentes. On se retrouve alors avec une image de dimension

(on garde les dimensions d'origine mais on a désormais trente-deux cartes de caractéristiques). On passe alors ces cartes de caractéristique dans une fonction d'activation, par exemple la fonction ReLU, puis le résultat est utilisé dans un max pooling qui va réduire la dimensionnalité de ces cartes. En utilisant un filtre de max pooling de deux pixels par deux, cette couche produit un résultat de dimension

(on garde le même nombre de cartes de caractéristiques mais on divise leurs dimensions par deux). On peut alors répéter cette opération jusqu'à obtenir des dimensions de cartes suffisamment réduites, quitte à augmenter le nombre de cartes, par exemple

. Les cartes sont ensuite « aplaties », lors de la phase de flattening, pour obtenir un vecteur unidirectionnel contenant

 valeurs. Ce vecteur est présenté à un FNN dense qui a dix neurones de sortie, un par chiffre possible de zéro à neuf. Le réseau complet est alors capable d'attribuer un chiffre à chaque image. On peut comparer le résultat obtenu avec le résultat attendu et procéder à une opération de rétropropagation du gradient pour optimiser les résultats.

Les CNN sont utiles pour la reconnaissance d'images, mais ils constituent également la première partie des « auto-encodeurs variationnels », modèles génératifs développés plus loin dans ce rapport. L'architecture U-Net, par exemple, est un CNN utilisé dans le monde médical pour la segmentation d'images cérébrales ou hépatiques ainsi que dans la création de contenus visuels, notamment par l'application Stable Diffusion.

(5) Les réseaux de neurones récurrents (RNN)

Dans les FNN, l'information ne circule que dans un sens, de l'entrée vers la sortie, comme il a été vu. De ce fait, chaque valeur d'entrée ne passe qu'une seule fois dans chaque couche de neurones du réseau. Ces réseaux ne peuvent pas traiter une séquence d'informations, c'est-à-dire des données provenant d'une série temporelle cohérente. On parle de données « dynamiques » en opposition aux données « statiques ». Ces données dynamiques englobent les vidéos, les graphiques d'évolution du cours d'actions en bourse, des relevés météorologiques, etc. Pour traiter ce type de données, il faut utiliser une architecture qui permette à des informations de « remonter » les couches du réseau. Les bases théoriques de ces types de réseaux ont été posées en 1972 par le japonais Shun'ichi Amari, on les nomme « réseaux de neurones récurrents » (en anglais recurrent neural networks ou RNN)^67(*). John Hopfield a été le premier à concevoir un tel réseau récurrent capable de traiter une information dynamique en 1982^68(*). Si l'information effectue au moins un cycle dans la structure du réseau, on a affaire à un RNN et plus à un FNN.

Un RNN ressemble à un réseau à propagation avant : il contient une couche d'entrée, des couches cachées et des couches de sortie. Il a toutefois la particularité de posséder une boucle de rétroaction : lorsqu'on lui présente successivement les données d'une séquence, le résultat obtenu pour une donnée prend en compte les résultats obtenus pour les données précédentes. Par exemple, si l'on utilise un RNN pour réaliser des prévisions météorologiques du lundi au dimanche, alors la boucle va permettre de prendre en compte le temps de lundi pour prédire le temps de mardi, le temps de lundi et mardi pour prédire celui de mercredi, etc.

On peut représenter un tel réseau de deux façons :

- selon un schéma « plié » du réseau, qui montre son fonctionnement de façon synthétique. Pour chaque entrée

, le réseau renvoie une sortie

ainsi qu'un certain nombre de paramètres qui vont être utilisés dans la couche cachée qui va traiter l'entrée

et donc avoir une influence sur la sortie

 ;

- selon une version « dépliée » du schéma, qui montre plus clairement l'influence du traitement de chaque entrée sur le traitement de l'entrée suivante. Pour parler de la phase traitée par les couches cachées et influençant les couches cachées à l'état

, on utilise le terme « état caché ».

Schéma d'un réseau de neurones récurrent

Ce modèle peut être entraîné de la même façon qu'un réseau de neurones à action directe grâce à la technique de rétropropagation du gradient. Toutefois, le calcul du gradient prend en compte un paramètre supplémentaire : l'information provenant des étapes précédentes de la séquence. La prise en compte de ce nouveau paramètre crée deux problèmes opposés : d'une part, un risque de « disparition du gradient » (en anglais gradient vanishing), situation où le gradient devient très faible et ne modifie quasiment plus les poids et les biais du modèle ; d'autre part, un risque d'« explosion du gradient », situation où, au contraire, le gradient devient très fort et modifie les poids et les biais de façon erratique. Ces problèmes rendent le gradient inopérant à long terme, ce qui empêche les RNN simples de traiter l'information de façon cohérente sur une longue séquence. Pour pallier ces problèmes, l'architecture des RNN a dû être améliorée pour posséder une mémoire à court terme, mais également une mémoire à long terme.

(6) Les réseaux de neurones à mémoire court et long terme (LSTM)

Les RNN donnent de bons résultats pour une mémoire courte par exemple pour assurer la prédiction du mot de la phrase suivante « La couleur du ciel est ...... » mais pour une phrase plus longue comme « J'ai passé vingt longues années à travailler pour les enfants défavorisés en Espagne. J'ai ensuite déménagé en Afrique. Je parle couramment ......... », les RNN sont en difficulté car l'information se propage dans le réseau puis se perd à cause du problème de la disparition du gradient (vanishing gradient)^69(*).

Les réseaux de neurones à mémoire court et long terme (en anglais long-short term memory ou LSTM) sont une architecture de RNN qui permet de résoudre les problèmes de disparition et d'explosion du gradient.

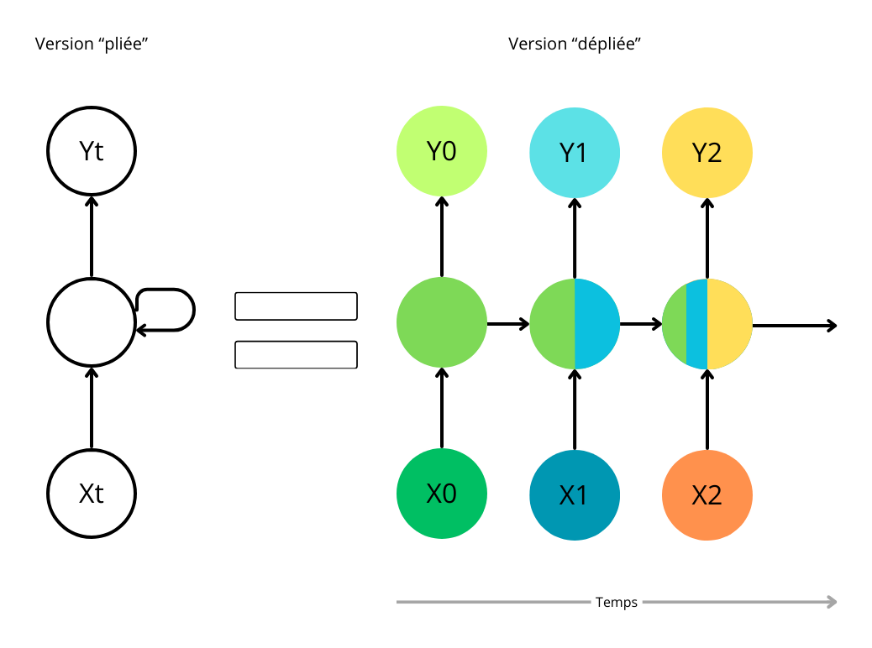
Cette architecture, qui est la plus utilisée en pratique, a été inventée en 1997 par Sepp Hochreiter et Jürgen Schmidhuber^70(*). L'information passe par trois portes : une porte d'entrée (input gate), une porte de sortie (output gate) et une porte d'oubli (forget gate).

Schéma simplifié d'une cellule de LSTM et de ses trois portes

Source : Omar Imai, op. cit.

Chaque unité computationnelle est liée non seulement à un état caché du réseau mais également à un état de la cellule qui joue le rôle de mémoire. Ainsi, les informations passant dans les cellules LSTM sont traitées selon une forme de mémoire : alors que certaines informations sont gardées à long terme, d'autres sont oubliées et ne passent donc pas au jalon temporel suivant.

Les réseaux RNN complétés de ces cellules LSTM ont notamment débouché sur les architectures Transformer qui sont à la base des Large Language Models et qui seront traitées plus loin.

c) Les autres systèmes d'apprentissage

D'autres systèmes ont précédé le Deep Learning et peuvent parfois présenter moins d'intérêt mais ils restent pertinents, par exemple dans des cas d'usage où la puissance des réseaux de neurones profonds n'est pas nécessaire.

(1) Les machines à vecteurs de support (SVM)

Les machines à vecteurs de support (support vector machines ou SVM, parfois traduits en « séparateurs à vaste marge » pour reprendre l'acronyme anglais) sont des moyens de classifier une population en groupes dont les individus sont similaires au regard d'un certain nombre de variables.

Ils correspondent à une généralisation des classifieurs linéaires. Leurs développements en informatique remontent aux années 1990, à la suite des travaux de théorie statistique conduits par Vladimir Vapnik en URSS depuis les années 1960 (menant notamment à la théorie de Vapnik-Chervonenkis, dite VC). Ils reposent ainsi sur les notions de marge maximale^71(*) et de fonction noyau^72(*), qui leur préexistaient, mais qu'ils sont les premiers à articuler.

Ces modèles sont efficaces dans le cas de données de grandes dimensions et peuvent donner des résultats équivalents à ceux des réseaux de neurones. Ils nécessitent de posséder un large jeu de données d'entraînement (individus dont on connaît a priori les variables d'intérêt et la classe) ; grâce auquel il devient possible de prédire la classe d'autres individus dont on ne connaît que les variables d'intérêt. Les individus peuvent être représentés comme des points dans un espace qui compte autant de dimensions que le nombre de variables requis pour décrire un individu.

Il s'agit de trouver la frontière séparant la population en deux classes. Deux types de situations se présentent alors : le cas où l'on peut séparer les classes de façon linéaire, c'est-à-dire où l'on peut déterminer un hyperplan dans l'espace tel que tous les individus d'une classe sont situés d'un côté de l'hyperplan et tous les individus de l'autre classe sont situés de l'autre côté ; le cas où l'on ne peut pas le faire et où la détermination de la frontière étant plus délicate, il faut trouver un autre moyen de séparer les classes de la population.

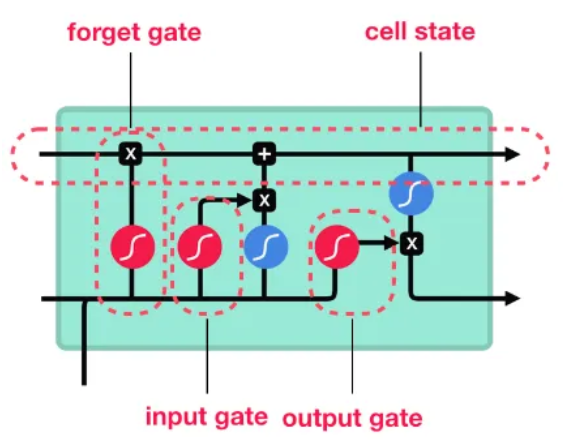
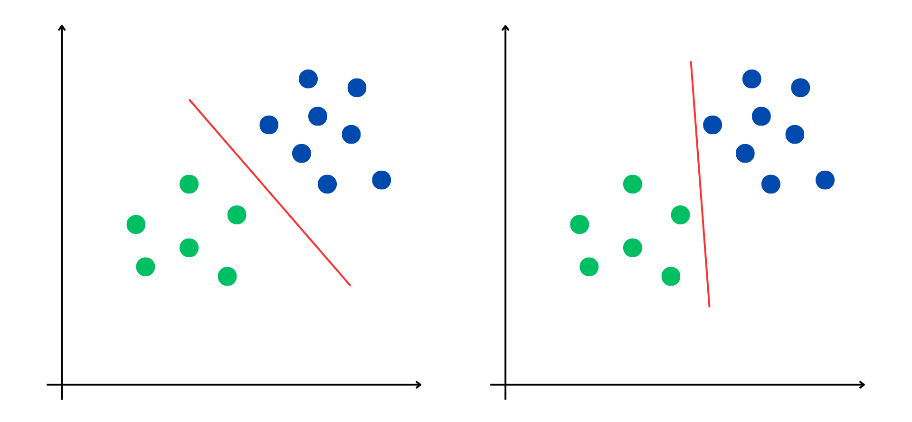
Deux exemples de classement (selon une visualisation géométrique)

Classement linéaire possible	Classement linéaire impossible regroupement dans un cercle

Néanmoins, il existe le plus souvent plusieurs possibilités de séparer une population en deux classes : c'est le cas des deux frontières rouges séparant la population en deux classes dans l'illustration ci-dessous.

Deux frontières possibles pour une même classification

Ces deux frontières semblent aussi performantes l'une que l'autre à l'issue de leurs processus d'apprentissage respectifs : le jeu de données d'apprentissage est correctement séparé en deux classes. Mais il reste à déterminer un moyen d'obtenir la frontière la plus pertinente, une séparation optimale qui permettrait, lorsqu'on ajoute à la population un nouvel individu n'appartenant pas au jeu d'entraînement, de déterminer sa classe avec un niveau de confiance élevé.

La frontière la plus pertinente avec un nouvel individu

Les deux frontières sont aussi performantes l'une que l'autre à l'issue de leurs processus d'apprentissage respectifs, mais leurs performances ne sont pas équivalentes quand on généralise l'usage du modèle avec l'entrée de nouveaux individus. Il reste à optimiser cette frontière.

Pour toute frontière possible, on peut déterminer la distance qui sépare un individu de cette frontière et, par voie de conséquence, quels sont les individus les plus proches de celle-ci. Leur distance à la frontière est appelée « marge ». La frontière optimale sera celle pour laquelle la marge est la plus grande. Une fois ce problème d'optimisation résolu :

- on dispose de la frontière, c'est-à-dire de la règle de classement, qui classera le mieux les individus autres que ceux de l'ensemble d'apprentissage ;

- pour chacune des deux classes, il existe un individu au moins qui est le plus proche de la frontière. Et ces individus sont appelés « vecteurs de support », on peut les voir comme les représentants de leurs classes car si l'échantillon d'apprentissage n'était constitué que par ces vecteurs de support, la frontière optimale que l'on trouverait alors serait identique à la précédente : les vecteurs de support contiennent toute l'information qui détermine la frontière ou règle de classement.

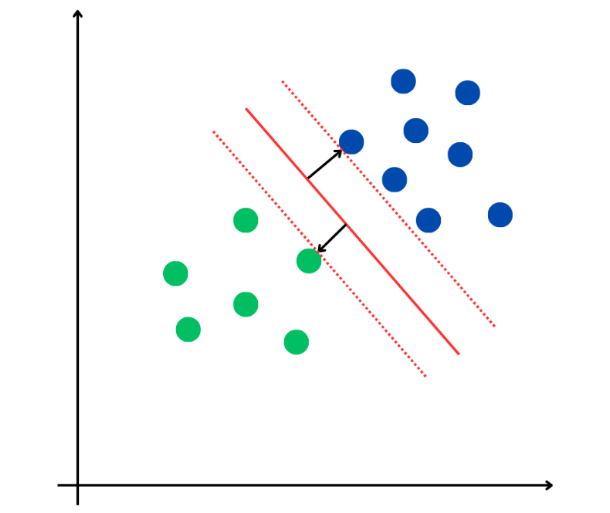
Le frontière optimale correspondant aux vecteurs de support

La frontière (ligne rouge continue) classe ici la population de façon optimale : tous les individus de chaque groupe sont répartis de part et d'autre et la marge est maximale (distance entre la frontière et les individus bleu et vert les plus proches, appelés vecteurs de support, marqués par une flèche noire). De chaque côté de la frontière, il existe un hyperplan parallèle à celle-ci qui passe par le ou les individus de support (lignes rouges pointillées) et la frontière la plus pertinente est située à égale distance de ces deux hyperplans.

Le grand intérêt de la notion de « vecteurs de support » est qu'elle permet de généraliser l'utilisation de machines SVM à des populations qui ne sont pas linéairement séparables. En toute rigueur, aucune frontière n'est capable de séparer complètement et exactement ce type de population entre deux classes déterminées : tout hyperplan de l'espace laissera « du mauvais côté » au moins un individu. Deux approches sont possibles dans cette situation.

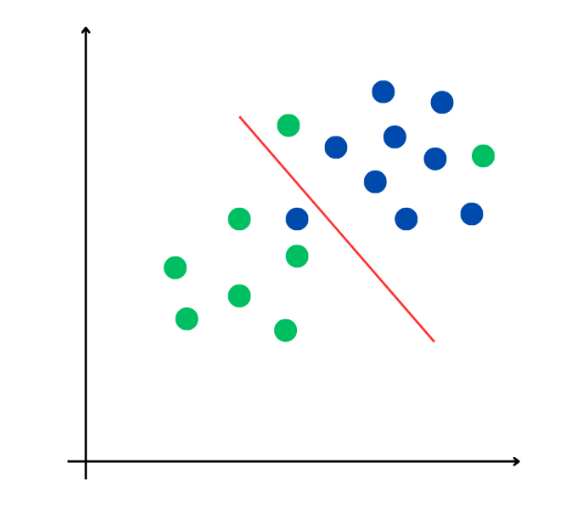
On peut d'abord accepter le fait que la règle de classement (ou la frontière) génère quelques erreurs, mais faire en sorte que leur portée reste limitée. On met alors en oeuvre la méthode des séparateurs à « marges souples ». Le processus d'optimisation permettant de déterminer la frontière optimale fonctionne alors sous double contrainte : comme précédemment, il faut maximiser la marge, mais désormais il faut aussi minimiser une fonction d'erreur, assise sur l'écart entre le classement généré par la machine et le classement effectif, pour chaque individu du jeu d'entraînement. Un paramètre nouveau définit la tolérance de la machine aux erreurs ; en pratique, plusieurs machines sont souvent construites, avec différentes valeurs du paramètre de tolérance, puis l'on choisit la plus acceptable. Le graphique suivant illustre un séparateur à marges souples. La frontière qui sépare les deux classes de la population est optimale tout en faisant apparaitre trois individus mal classés (deux verts et un bleu).

Le seuil optimal selon un séparateur à marges souples

La seconde méthode consiste à effectuer une séparation exacte, mais non linéaire. Elle suppose d'ajouter des dimensions supplémentaires à l'espace des données décrivant les individus, de façon à obtenir un espace dans lequel il est certain que la population peut être linéairement séparée^73(*). On détermine alors la frontière optimale dans ce nouvel espace, selon la méthode SVM exposée ci-dessus, puis on en déduit la frontière dans l'espace des données initial.

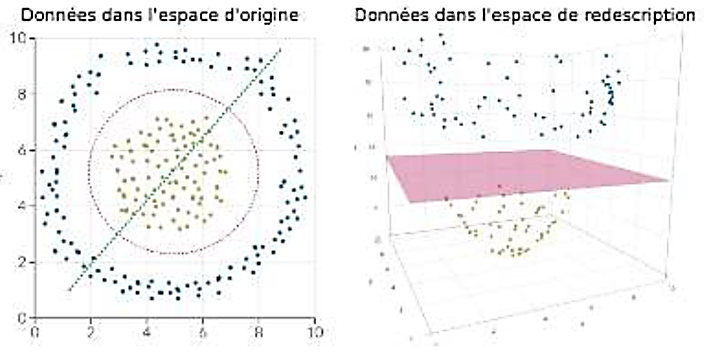
Le passage par un espace de redescription

Source : Jean-Paul Comet, septembre 2024, Cours d'introduction à l'IA pour la biologie, Université de Nice-Sophia-Antipolis, cf. https://webusers.i3s.unice.fr/~comet/SUPPORTS/index.php

Dans l'espace d'origine ici à deux dimensions, la population n'est pas linéairement séparable, mais dans l'espace de redescription (ici à trois dimensions), on peut trouver l'hyperplan qui correspond à la frontière optimale. Ramené à l'espace initial à deux dimensions, cet hyperplan dessine un cercle.

(2) Les modèles markoviens ou « chaînes de Markov »

Les algorithmes d'intelligence artificielle peuvent reposer sur certaines prédictions stochastiques modélisant des processus aléatoires, appelées modèles markoviens ou « chaînes de Markov », dont le processus de Bernoulli est l'un des exemples les plus connus, représentant la forme la plus simple de ces calculs. Il s'agit de probabilités pour lesquelles les états futurs ne dépendent que de l'état présent et pas des états antérieurs^74(*). Cette absence de besoin de mémoire du passé est appelée « propriété de Markov ». Si cette propriété est présente parmi des variables aléatoires, on a affaire à un « processus de Markov ». Si ce processus correspond à des états qui sont dénombrables (autrement dit si l'on a affaire à un espace discret), il s'agit d'une « chaîne de Markov ».

Sous réserve de disposer de nombreuses variables (ces prédictions sont soumises à la loi des grands nombres), ces modèles peuvent donner des résultats significatifs, comme l'a montré leur utilisation fréquente en physique statistique depuis le début du XX^e siècle. Les systèmes de bonus-malus des assurances les utilisent. L'algorithme PageRank qui a fait le succès de Google et qui permet à son moteur de recherche de classer les pages Web selon leur popularité repose sur une chaîne de Markov. De tels modèles peuvent aussi produire du texte, en suggérant une suite de mots.

Partons d'un processus de Markov avec des états dans lesquels on a une variable aléatoire X et un processus aléatoire par lequel l'état de X_n+1 est déterminé par X_n, l'état futur dépendant donc de l'état présent. Dans un tel processus, il est possible de réaliser une « chaîne de Markov » qui représente les transitions possibles entre ces états. Le plus souvent cette chaîne est représentée par une matrice de transition mais on peut aussi la figurer dans un schéma.

Un exemple de chaîne de Markov issu de la vie quotidienne pourrait être, en le simplifiant, la météorologie. Avec des prévisions qui seraient réduites à seulement trois états possibles (« ensoleillé », « nuageux » et « pluvieux »), on part de l'état actuel - la météo du jour - qui peut être l'une de ces trois conditions météorologiques. Or l'état du lendemain dépend de l'état actuel : il est moins probable de passer d'un temps ensoleillé à un temps pluvieux que de passer d'un temps ensoleillé à un temps nuageux. En observant les conditions climatiques aux instants T+1, T+2 ... jusqu'à T+N, on a une chaîne d'événements probables. Cette chaîne est markovienne puisque la probabilité du temps qu'il fera demain est déterminée par le temps qu'il fait aujourd'hui.

On a un modèle de Markov caché (MMC) lorsque l'on a une chaîne de Markov dont on connaît les probabilités de transition entre les différents états mais pour lequel les états sont cachés, ainsi que des variables observables dépendant de variables cachées. On connaît simplement de ces variables observées la probabilité de les observer en fonction de l'état de la variable cachée. Ainsi, l'état de la variable cachée influence la variable observable, mais l'inverse n'est pas exact.

Ces modèles tentent de comprendre une réalité qui reste partiellement voilée par des incertitudes. Dans un modèle de Markov caché, deux mondes coexistent : le monde caché, qui évolue selon certaines règles, et le monde visible, où nous faisons nos observations. Le défi réside dans l'absence d'accès direct aux états du monde caché : avec des indices observables laissés derrière lui, ce monde peut être approché.

Pour déchiffrer la séquence des états cachés d'un MMC, il faut calculer la probabilité des états cachés en fonction des observations visibles, puis utiliser le théorème de Bayes pour établir une probabilité conditionnelle et calculer les nouveaux termes de probabilité avec une approche récursive, appelée algorithme de progression ou algorithme avant (forward algorithm). La probabilité de chaque état est sans cesse affinée, et l'on arrive à un modèle qui associe chaque observation à une série d'états cachés, dévoilant ainsi partiellement ce qui ne pouvait pas être vu directement : inférer les états cachés a permis de finaliser l'interprétation.

Pour illustrer un modèle de Markov caché, on peut prendre l'exemple d'une ville dont on ne connaît pas la météo mais seulement les probabilités de transition entre différents états, en simplifiant à nouveau avec trois possibilités : « ensoleillé », « nuageux » et « pluvieux ». Régulièrement, on organise une visioconférence avec Eliza, une habitante de la ville dont on sait qu'elle peut être soit heureuse, soit malheureuse. On sait également que l'humeur d'Eliza dépend du temps, et on connaît la probabilité de l'humeur d'Eliza en fonction du temps qu'il fait dans sa ville. On observe pendant plusieurs jours l'humeur d'Eliza et en fonction de cela, on détermine la combinaison de temps la plus probable pour aboutir à cette suite d'humeurs. Dans cet exemple, la variable cachée est le temps qu'il fait dans la ville d'Eliza, et la variable observable est l'humeur d'Eliza. Il est possible de déterminer l'état probable de la variable cachée grâce à la variable observable.

(3) La contribution des réseaux bayésiens à l'IA

Les réseaux bayésiens, en référence au mathématicien britannique Thomas Bayes^75(*), sont des modèles graphiques probabilistes représentant un ensemble de variables aléatoires, sous la forme d'un graphe orienté acyclique (de l'anglais Directed Acyclic Graph - DAG). Dans ce graphe, les relations de cause à effet entre les variables ne sont pas déterministes, mais probabilisées. Le réseau bayésien devient une sorte de machine à calculer des probabilités conditionnelles. En fonction des informations observées, la probabilité des données non observées peut être calculée^76(*). L'utilisation d'un tel réseau s'appelle « inférence ». Il s'agit d'un calcul de probabilités a posteriori, étant donné des nouvelles informations observées.

Ces réseaux peuvent être utilisés en Machine Learning puisqu'à partir des données, il devient possible d'estimer la structure d'un réseau ou les tables de probabilités d'un réseau. Par le calcul des inférences dans des réseaux bayésiens, il est possible d'aider au diagnostic, tant en matière médicale qu'industrielle, notamment grâce à l'analyse de risques. Les réseaux bayésiens permettent aussi à des systèmes d'IA de faire de la détection des spams ou du data mining.

D'autres méthodes probabilistes, parfois utilisées en IA, reposent sur ces modélisations bayésiennes, à l'instar de la « méthode de Monte-Carlo par chaînes de Markov » (MCMC pour Markov chain Monte Carlo en anglais) algorithme à ne pas confondre avec « l'algorithme de Monte-Carlo » (qui utilise une source de hasard). Les MCMC utilisent la méthode de Monte-Carlo (qui permet de calculer une valeur numérique approchée en utilisant des procédés aléatoires, c'est-à-dire des techniques probabilistes, dans le but par exemple d'introduire des risques) mais en se basant sur le parcours de chaînes de Markov, qui ont pour lois stationnaires les distributions à échantillonner.

(4) L'apport de la « régularisation statistique » de Vapnik

Les réseaux de neurones formels, les modèles de Markov cachés mais aussi tous les autres modèles statistiques classiques utilisent soit des méthodes d'optimisation directe, comme la régression linéaire, soit des méthodes itératives comme la descente du gradient. Or tous les systèmes d'apprentissage font face à des problèmes de surapprentissage, on parle aussi parfois de surajustement ou de surinterprétation. Le modèle devient trop précis car il contient plus de paramètres que les données ne le justifient. Vladimir Vapnik, l'inventeur des SVM, a répondu au problème dans l'URSS des années 1970 et 1980 avec sa théorie de la régularisation statistique.

Pour réduire la variance des modèles, on introduit de nouvelles informations permettant par exemple de pénaliser les valeurs extrêmes des paramètres. Le plus souvent, il s'agit d'utiliser une norme sur ces paramètres, que l'on va ajouter à la fonction qu'on cherche à minimiser. L'optimisation devient alors possible en évitant ou du moins en réduisant les phénomènes de surapprentissage.

---

* ³⁹ Shortliffe, Edward H, et Bruce G Buchanan. 1975. « A model of inexact reasoning in medicine ». Mathematical biosciences 23(3-4): 351-79.

* ⁴⁰ En informatique, une ontologie est la modélisation d'un ensemble de données par des concepts et relations issues de connaissances dans un domaine donné (par exemple, géographie, médecine, agriculture, etc.), source : Cnil.

* ⁴¹ Le Web sémantique consiste en un Internet intelligent permettant aux ordinateurs de comprendre et de répondre aux demandes de l'utilisateur en fonction du sens de celles-ci. Cette structure de connaissances aurait été accessible aux machines en insérant sur les pages Web des métadonnées lisibles par l'ordinateur. Ces métadonnées étant liées les unes aux autres, le Web sémantique aurait conduit à des usages plus intelligents d'Internet. Des langages ont été conçus à cette fin, comme RDF (Resource Description Framework), OWL (Ontology Web Language) ou XML (eXtensible Markup Language) mais la faisabilité d'une telle technologie d'IA à l'échelle des milliards de pages d'Internet devient de plus en plus difficile. Par exemple, l'ontologie de la terminologie médicale SNOMED CT contient à elle seule 370 000 noms de classes or aucune technologie existante n'a été en mesure d'éliminer tous les doublons du point de vue sémantique. Les applications de ces systèmes resteront donc surtout réservées au monde des bibliothèques, à l'édition ou à des blogs spécialisés. La Bibliothèque nationale de France utilise ainsi en lien avec sa bibliothèque numérique Gallica, un système de Web sémantique à travers le projet « data.bnf.fr », basé sur un réseau de métadonnées sous la forme de triplets RDF contenus dans chaque URL. Depuis 2017, le système data.bnf.fr s'appuie sur le modèle conceptuel de référence au niveau international, dit « IFLA LRM »).

* ⁴² Cf. John Searle, 1980, « Minds, brains, and programs », Behavioral and Brain Sciences, vol. 3, n° 3 : https://www.cambridge.org/core/journals/behavioral-and-brain-sciences/article/abs/minds-brains-and-programs/DC644B47A4299C637C89772FACC2706A. François Chollet, chercheur en intelligence artificielle et créateur de la bibliothèque Keras, sans commenter l'expérience de la chambre chinoise, a abordé des questions similaires concernant la nature de la compréhension de l'intelligence artificielle et ce que l'on appelle l'intelligence des machines. Dans son article « On the Measure of Intelligence », il proposait en 2019 une définition de l'intelligence basée sur l'efficacité de l'acquisition de compétences, soulignant que la simple exécution de tâches ne reflète pas une véritable compréhension ou intelligence.

* ⁴³ Dans ses Fragments, Héraclite, penseur du mouvement niant le principe d'identité, distinguait déjà la pensée (ã?äïò), l'énoncé (?ðïò) et la réalité (?ñãïí), la liaison entre ces trois éléments étant réalisée selon lui par le logos, principe unique d'essence divine.

* ⁴⁴ Les superstatistiques au sens strict forment un sous-domaine de la physique statistique et consistent à décrire les propriétés statistiques d'un système par une superposition de statistiques.

* ⁴⁵ Les notions de « couche cachée » et de « fonction d'activation » sont abordées plus loin.

* ⁴⁶ Cybenko, George. 1989. « Approximation by superpositions of a sigmoidal function ». Mathematics of control, signals and systems.

* ⁴⁷ Hornik, Kurt, Maxwell Stinchcombe, et Halbert White. 1989. « Multilayer feedforward networks are universal approximators » et, 1991, « Approximation capabilities of multilayer feedforward networks », Revue Neural networks.

* ⁴⁸ Il existe plusieurs extensions du théorème, notamment aux domaines non compacts, aux architectures de réseaux et topologies alternatives, ou encore à des réseaux certifiables. Cf. Patrick Kidger et Terry Lyons, 2020, « Universal Approximation with Deep Narrow Networks », Conference on Learning Theory, Hongzhou Lin et Stefanie Jegelka, 2018, « ResNet with one-neuron hidden layers is a Universal Approximator », Advances in Neural Information Processing Systems, Maximilian Baader, Matthew Mirman et Martin Vechev, 2020, « Universal Approximation with Certified Networks », ICLR.

* ⁴⁹ McCulloch, Warren S, et Walter Pitts, 1943, « A logical calculus of the ideas immanent in nervous activity », Bulletin of Mathematical Biophysics, n^o 5,ý pp. 115-133.

* ⁵⁰ Cf. J. Lettvin, H. Maturana, W. McCulloch et W. Pitts, « What the Frog's Eye Tells the Frog's Brain », Proceedings of the IRE, vol. 47, n^o 11,ý novembre 1959, pp. 1940-1951.

* ⁵¹ Frank Rosenblatt, 1958, « The perceptron : a probabilistic model for information storage and organization in the brain », Psychological review, vol. 65, n° 6.

* ⁵² On parle « d'hyperplan » pour parler d'espaces avec une dimension de moins que l'espace dans lequel on se trouve. En deux dimensions, il s'agit d'une droite (une dimension), en trois dimensions, d'un plan (deux dimensions), on peut étendre le principe aux espaces à plus de dimensions.

* ⁵³ Cf. John J. Hopfield, 1982, « Neural networks and physical systems with emergent collective computational abilities », Proceedings of the National Academy of Sciences, vol. 79, n° 8 : https://www.pnas.org/doi/10.1073/pnas.79.8.2554

* ⁵⁴ Cf. Marvin L Minsky. et Seymour A. Papert, 1969, Perceptrons : an introduction to computational geometry. éd. Cambridge MIT Press.

* ⁵⁵ La notion d'alternance entre « Hivers » et « Printemps » de l'IA a été plus amplement développée dans le rapport de l'OPECST écrit par M. le député Claude de Ganay et Mme la sénatrice Dominique Gillot : Pour une intelligence artificielle maîtrisée, utile et démystifiée disponible sur le site du Sénat : https://www.senat.fr/rap/r16-464-1/r16-464-11.pdf et de l'Assemblée nationale : https://www2.assemblee-nationale.fr/documents/notice/14/rap-off/i4594/(index)/index-thematique-oecst

* ⁵⁶ Cf. ces deux articles fondateurs : David Rumelhart, Geoffrey Hinton et Ronald Williams, 1986, « Learning representations by back-propagating errors », Nature, vol. 323 ; David Rumelhart, Geoffrey Hinton, et James McClelland, 1986, « A general framework for parallel distributed processing » in David Rumelhart et James McClelland, Parallel distributed processing: Explorations in the microstructure of cognition, MIT Press.

* ⁵⁷ C'est l'objet même de la thèse de Yann LeCun et l'un des enjeux de celle de Yoshua Bengio. Cf. Yann LeCun, 1987, « Modèles connexionnistes de l'apprentissage », thèse de doctorat, Université Paris VI, Paris, ainsi que plus spécifiquement Yann LeCun, 1988, « A Theoretical Framework for Back-Propagation », Proceedings of the 1988 Connectionist Models Summer School, Carnegie Mellon University, Pittsburg. Yann LeCun a également introduit les réseaux neuronaux convolutifs (CNN). Et pour Yoshua Bengio: Yoshua Bengio, 1991, « Artificial neural networks and their application to sequence recognition », Mc Gill University, Montréal, ainsi que plus spécifiquement Yoshua Bengio et al., 1994, « Learning long-term dependencies with gradient descent is difficult », IEEE Transactions on Neural Networks, volume 5, n° 2.

* ⁵⁸ La rétropropagation neuronale désigne la propagation d'un potentiel d'action dans un neurone, non pas vers la terminaison de l'axone (propagation normale), mais au rebours, en direction des dendrites, d'où provenait la dépolarisation originelle. Cf. Greg Stuart, Nelson Spruston, Bert Sakmann et Michael Häusser, 1997, « Action potential initiation and backpropagation in neurons of the mammalian CNS », Trends in Neurosciences, vol. 20, n° 3 : https://pubmed.ncbi.nlm.nih.gov/9061867/

* ⁵⁹ Cf. Yann LeCun, Yoshua Bengio, et Geoffrey Hinton, 2015, « Deep Learning », numéro spécial de la revue Nature.

* ⁶⁰ Hubel, David H, et Torsten N Wiesel. 1968. « Receptive fields and functional architecture of monkey striate cortex ». The Journal of physiology 195(1): 215-43.

* ⁶¹ Kunihiko Fukushima, 1975, « Cognitron: A self-organizing multilayered neural network », Biological cybernetics, 20(3): 121-36.

* ⁶² Kunihiko Fukushima, 1980, « Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position », Biological cybernetics 36(4): 193-202.

* ⁶³ Yann LeCun, 2019, Quand la machine apprend : La révolution des neurones artificiels et de l'apprentissage profond, Odile Jacob. pp. 203-204.

* ⁶⁴ Yann LeCun, Léon Bottou, Yoshua Bengio, et Patrick Haffner, 1998, « Gradient-based learning applied to document recognition », Proceedings of the IEEE.

* ⁶⁵ Kaiming He, Zhang Xiangyu, Ren Shaoqing et Sun Jian, 2016, « Deep residual learning for image recognition ».

* ⁶⁶ Voir le tableau des fonctions d'activation pour une liste non exhaustive des fonctions d'activation qu'il est possible d'utiliser.

* ⁶⁷ S-I Amari, 1972, « Learning patterns and pattern sequences by self-organizing nets of threshold elements », IEEE Transactions on computers.

* ⁶⁸ John J. Hopfield, 1982, « Neural networks and physical systems with emergent collective computational abilities », Proceedings of the National Academy of Sciences.

* ⁶⁹ L'exemple est tiré de l'article suivant d'Omar Imai relatif aux réseaux de neurones récurrents à mémoire court terme et long terme : https://medium.com/@pcomarimai/les-r%C3%A9seaux-de-neurones-r%C3%A9currents-%C3%A0-m%C3%A9moire-court-terme-et-long-terme-lstm-e8b4f83f4ab

* ⁷⁰ Sepp Hochreiter et Jürgen Schmidhuber, 1997, « Long short-term memory ». Neural computation.

* ⁷¹ C'est la frontière séparatrice optimale entre les différents échantillons de la population.

* ⁷² Cette astuce, dite Kernel Trick en anglais, consiste à simplifier le produit scalaire (celui des n vecteurs contenus dans l'espace vectoriel complexe de grande dimension que forment les échantillons de données) en une simple fonction type, appelée fonction noyau, permettant d'éviter l'explosion combinatoire du nombre de paramètres. Les deux fonctions les plus utilisées sont le noyau gaussien et, surtout, le noyau polynomial (il utilise les similarités entre les vecteurs ainsi qu'entre leurs combinaisons). On retrouve un procédé similaire en mathématiques avec les opérateurs intégraux qui permettent de résoudre des équations intégrales.

* ⁷³ Ce nouvel espace s'appelle « espace de redescription », ou « espace transformé », ou encore « espace des caractéristiques ». Selon le problème posé, il peut être nécessaire de prendre un espace de redescription ayant un nombre infini de dimensions.

* ⁷⁴ La capacité à prédire le futur à partir du présent n'est pas améliorée par des informations supplémentaires relatives au passé. Dans ces calculs de probabilité, toute l'information utile à la prédiction du futur est présente dans les états actuels.

* ⁷⁵ Le théorème de Bayes, dérivé en 1763 de la théorie des probabilités conditionnelles et utilisé pour le calcul de probabilités ainsi que pour les statistiques, permet de déterminer la probabilité qu'un événement arrive à partir d'un autre événement qui s'est réalisé, notamment quand ces deux événements sont interdépendants. Nécessitant un grand nombre de calculs, les inférences bayésiennes se sont surtout développées grâce à l'informatique. Le mathématicien français Laplace a formulé la même théorie un peu plus tard sans connaître les travaux de Bayes.

* ⁷⁶ Par exemple, en fonction des symptômes d'un malade, on calcule les probabilités des différentes pathologies compatibles avec ces symptômes. On peut aussi calculer la probabilité de symptômes non observés, et en déduire les examens complémentaires les plus nécessaires.